Non-dimensional solution

In this chapter we propose a non-dimensional formulation of the two-phase sediment transport equations and we show the necessary steps required in order to obtain a non-dimensional solution. First the governing equations in their non-dimensional form are presented. Afterward we demonstrate how to perform some of the SedFoam tutorials simulations using the non-dimensional formulation.

Non-dimensional governing equations

The non-dimensional formulation of the two-phase flow equations starts with the selection of characteristic quantities. In particular, a characteristic length and a characteristic velocity scale need to be selected. For example, in the case of a turbulent flow in an open channel, the channel height $x_c=H$ and the friction velocity $u_c=u_{\tau}$ , are usually selected. A characteristic timescale can then also be obtained as $t_c=H/u_{\tau}$ . The non-dimensional formulation of the turbulence-averaged two-phase flow governing equations is presented below. The characteristic quantities of the open channel flow are used in the derivation of the non-dimensional equations for the shake of convenience. Non-dimensional quantities are marked with an asterisk. The closure models for particle–particle interaction, flow turbulence, and turbulence–sediment interaction terms are those presented in the Governing equations section of this guide. For more details the interested reader is also referred to Chauchat et al. (2017).

The non-dimensional mass conservation equations for the particle phase and the fluid phase are written as:

\[ \frac{\partial \beta}{\partial t^*} + \frac{\partial \beta u_i^{*b}}{\partial x_i^*} = 0 \]
\[ \frac{\partial \alpha}{\partial t^*} + \frac{\partial \alpha u_i^{*a}}{\partial x_i^*} = 0 \]

where $x^*=x/H$ , $u^*=u/u_{\tau}$ and $t^*=tu_{\tau}/H$ .

The non-dimensional momentum equations for particle and fluid phases can be written as:

\[ \frac{\partial \alpha u_i^{*a}}{\partial t^*} + \frac{\partial \alpha u_i^{*a} u_j^{*a}}{\partial x_j^*} = - \frac{\alpha}{\rho^*} \frac{\partial p^*}{\partial x_i^*} - \frac{1}{\rho^*} \frac{\partial(p^{*ff} + p^{*a})}{\partial x_i^*} + \frac{1}{\rho^*} \frac{\partial \tau_{ij}^{*a}}{\partial x_j^*} + \frac{\alpha g_i^*}{Fr^2} + \frac{1}{\rho^*} \alpha \beta K^* (u_i^{*b} - u_i^{*a}) - \frac{S_{US}}{\rho^*} \beta K^* {C_\mu} \frac{k^{*2}}{\epsilon^*} \frac{\partial \alpha}{\partial x_i^*} \]
\[ \frac{\partial \beta u_i^{*b}}{\partial t^*} + \frac{\partial \beta u_i^{*b} u_j^{*b}}{\partial x_j^*} = - \beta \frac{\partial p^*}{\partial x_i^*} + \frac{\partial \tau_{ij}^{*b}}{\partial x_j^*} + \frac{\beta g_i^*}{Fr^2} - \alpha \beta K^* (u_i^{*b} - u_i^{*a}) + S_{US} \beta K^* {C_\mu} \frac{k^{*2}}{\epsilon^*} \frac{\partial \alpha}{\partial x_i^*} \]

where

\[ p^{*ff} = C^*_{Fr} \frac{(\alpha - \alpha^{min})^{\eta_0}}{( \alpha^{max} - \alpha)^{\eta_1}} \]
\[ p^{*a} = \rho^* \left( \frac{B_\phi \alpha}{\alpha^{max}-\alpha} \right)^2 d^{*2} ||\overline{\overline{S^{*a}}}||^2 \]
\[ \tau_{ij}^{*a} = \left[ \mu_S + \frac{\mu_2 - \mu_S}{I_0 B_\phi \alpha} (\alpha^{max}-\alpha) \right] \frac{S_{ij}^{*a}}{\sqrt{2(S_{ij}^{*a} \cdot S_{ij}^{*a})}} (p^{*ff} + p^{*a}) \]
\[ K^* = \frac{18}{Re_p} \left(1 + 0.15 Re_p^{0.687}\right) \frac{\|\mathbf{u}^{*b} - \mathbf{u}^{*a}\|}{\rho^* d^* \psi} \beta^{-h_{\text{exp}}} \]
\[ Re_p = \beta \|\mathbf{u}^{*b} - \mathbf{u}^{*a}\| d^* \psi Re_\tau \]
\[ \tau_{ij}^{*b} = 2 C_\mu \frac{k^{*2}}{\epsilon^*} S_{ij}^{*b} + \frac{2}{Re_\tau} \left[ 1 + 2.5 \alpha \left( 1 - \frac{\alpha}{\alpha^{max}} \right)^{-1} \right] S_{ij}^{*b} - \frac{2}{3} k^* \]

with $p^* = p /(\rho^b u_\tau^2)$ the non-dimensional pressure, $C^*_{Fr} = C_{Fr} / (\rho^b u_\tau^2)$ the non-dimensional counterpart of the coefficient in the permanent particle contact model, $g^*$ the unit vector in the direction of gravity, $k^* = k / u_\tau^2$ the non-dimensional turbulent kinetic energy and $\epsilon^* = \epsilon H / u_\tau^3$ the non-dimensional turbulent kinetic energy dissipation rate. The following additional non-dimensional parameters appear in the above equations: the Reynolds number, $Re_\tau = H u_\tau / \nu^b$ describing the ratio between inertia and viscous forces, the Froude number, $Fr = u_\tau / \sqrt{g H}$ describing the ratio between inertia and gravity forces, the non-dimensional particle diameter, $d^* = d / H$ and the ratio between particle and fluid phase density, $\rho^* = \rho^a / \rho^b$ . In this way, the general sediment transport turbulent flow problem is reduced to the minimum set of independent parameters. Indeed, according to Buckingham $\pi$ theorem the parameter space of the problem is reduced from the original dimensional N = 7: $f(H, u_\tau, \rho^b, \eta^b, g, d, \rho^\alpha)$ to the M = 7 - 3 = 4: $g(Re_\tau, Fr, \rho^*, d^*)$ non-dimensional parameter space. Note that other non-dimensional groups can be used to describe sediment transport in turbulent flow instead of the above four, however any additional non-dimensional group will necessarily be a dependent parameter of this original set of four. For example, the following non-dimensional groups can also be defined (among others): Stokes number, $Stk = \rho^* Re_\tau d^{*2} / 18$ (assuming a Stokes flow regime) describing the ratio between particle response time and characteristic time scale of the flow, Suspension number $S = (\rho^* - 1) Re_\tau d^* / {(18 Fr^2)}$ (assuming a Stokes flow regime) describing the ratio between the particle settling velocity and the characteristic velocity of the flow and Shields number $\theta = Fr^2 / [(\rho^* - 1) d^*]$ describing the ratio between forces acting to mobilize sediment particles on a bed to the resisting forces due to the particle's weight.

Non-dimensional solution tutorials

The following tutorials show how to run the sedFOAM tutorials in order to obtain a non-dimensional instead of a dimensional solution. Note that there is no required modification in the flow solver. The parameters in the input files only need to be modified in such a way as to obtain the corresponding non-dimensional terms in the mass and momentum equations. The non-dimensional version of three of the original sedFOAM tutorials is demonstrated below. Namely: 1DSedim: Pure sedimentation, 1DSheetFlow: Turbulent sheet-flows and 3DChannel560: Turbulent channel flow laden with particles. In the following, only the lines that require modification in the corresponding input files of the tutorials are presented. For more details about the set-up and execution of these tutorials the reader is referred to the original version of the tutorials in this guide.

nd1DSedim: Pure sedimentation

The laminar flow tutorial - 1DSedim: Pure sedimentation is found in the folder sedFoamDirectory/tutorials/laminar/1DSedim. The following modifications need to be made in the tutorial input files in order to obtain a non-dimensional solution:

Mesh generation

The blockMeshDict in the folder system requires the following modification:

scale 1.0;
Boundary and initial conditions

The file 0_org/alpha.a requires the following modification:

forAll(mesh.C(), i)
        {
            scalar y = mesh.C()[i].y();
            if (y < 0.049/0.06)
            {
                alpha_a[i] = 0.5;
            }
            else
            {
                alpha_a[i] = 0.5*0.5*(1.0+tanh((y-0.054/0.06)/(0.0490/0.06-y)*10.0)); // nd domain profile
            }
        }
Physical properties

The physical properties in the file constant/transportProperties require the following modifications:

phasea
{
    rho             rho [ 1 -3 0 0 0 ] 1.1053; // rho* 
    nu              nu [ 0 2 -1 0 0 ] 0.0729;  // (1/Re)(nua/nub)
    d               d [ 0 1 0 0 0 0 0 ] 0.0048; // d*
}

phaseb
{
    rho             rho [ 1 -3 0 0 0 ] 1; // rhob/rhob 
    nu              nu [ 0 2 -1 0 0 ] 1.53; // 1/Re
    d               d [ 0 1 0 0 0 0 0 ] 0.0048; // d*
}

nu              nu [ 0 2 -1 0 0 0 0 ] 1.53; // 1/Re

nuMax           nuMax [0 2 -1 0 0 0 0] 1e6; // 1/Re (nu_max/nu_b)

The gravity properties in the file constant/g require the following modification:

value           ( 0 -11269566.57 0 ); // -1/Fr^2

The permanent particle contact properties in the file constant/ppProperties require the following modification:

Fr               Fr [ 1 -1 -2 0 0 0 0 ] 1007.7; // C_Fr/(rhob Ur^2)
Control

The simulation time control properties in the file system/controlDict require the following modifications:

endTime         10; // tend Ur / H

deltaT          1.0e-6; 

writeInterval   0.1; 

maxDeltaT       7.5e-4;
Running the simulation

Run the simulation using the shell script:

#!/bin/sh

# Create the mesh
blockMesh

# create the intial time folder
cp -r 0_org 0

# Run sedFoam
sedFoam_rbgh > log&
Postprocessing using fluidfoam

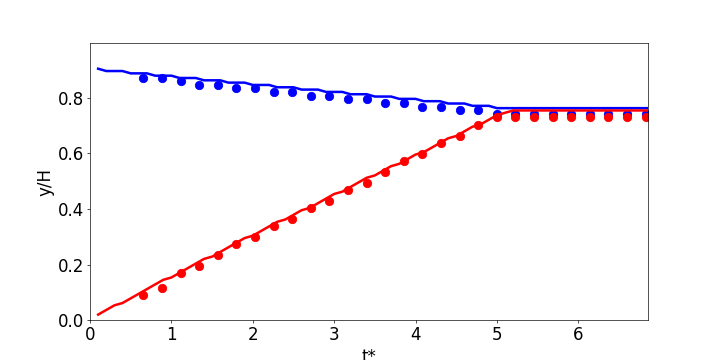
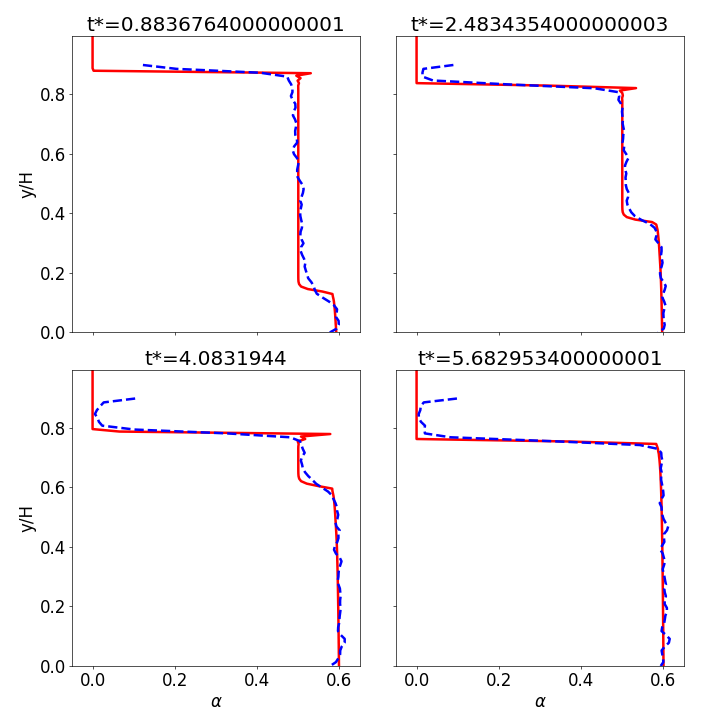
You just have to run the python script plot_nd_tuto1DSedim.py located in the folder tutorials/Py:

python plot_nd_tuto1DSedim.py

and you should see the following figures:

Image
Figure 2: Comparison of two-phase numerical results with experiments of Pham Van Bang et al. (2006) for the settling curves: time evolution of the lower and upper interface positions (circles: experiments ; lines: model).
Image
Figure 3: Comparison of two-phase numerical results with experiments of Pham Van Bang et al. (2006) for solid phase volume fraction profiles (dashed blue lines: experiment ; solid red lines: model).

nd1DSheetFlow: Turbulent sheet-flows

The RAS tutorial - 1DSheetFlow: Turbulent sheet-flows is found in the folder sedFoamDirectory/tutorials/RAS/1DSheetFlow. The following modifications need to be made in the tutorial input files in order to obtain a non-dimensional solution:

Mesh generation

The blockMeshDict in the folder system requires the following modification:

scale 1.0;
Boundary and initial conditions

The file 0_org/alpha.a requires the following modification:

alpha_a[i] = 0.53*0.5*(1.0+tanh((0.0211/0.17-y)/0.05/0.17*10.0)); // nd domain profile
Physical properties

The physical properties in the file constant/transportProperties require the following modifications:

phasea
{
    rho             rho [ 1 -3 0 0 0 ] 1.19; // rho* 
    nu              nu [ 0 2 -1 0 0 ] 0e0;
    d               d [ 0 1 0 0 0 0 0 ] 0.0176; // d*
}

phaseb
{
    rho             rho [ 1 -3 0 0 0 ] 1.0;  // rhob/rhob 
    nu              nu [ 0 2 -1 0 0 ] 1.18e-4; // 1/Re_tau
    d               d [ 0 1 0 0 0 0 0 ] 0.0176; // d*
}

nu              nu [ 0 2 -1 0 0 0 0 ] 1.18e-4; // 1/Re_tau

nuMax           nuMax [0 2 -1 0 0 0 0] 11.8; // nuMax/(u_tau H)

The pressure gradient force properties in the file constant/forceProperties require the following modification:

gradPMEAN        gradPMEAN        [ 1 -2 -2 0 0 0 0 ] (1.2675 0 0 ); // (DP/Dx) H / (rhob^2 u_tau^2)

The gravity properties in the file constant/g require the following modification:

value           ( 0 -667.0 0 ); // -1/Fr^2

The kinetic theory properties in the file constant/kineticTheoryProperties require the following modification:

MaxTheta       MaxTheta [ 0 2 -2 0 0 0 0 ] 4.0; // MaxTheta/u_tau^2

The permanent particle contact properties in the file constant/ppProperties require the following modification:

Fr               Fr [ 1 -1 -2 0 0 0 0 ] 2e-2; // C_Fr/(rhob u_tau^2)

The turbulence model properties in the file constant/turbulenceProperties.b require the following modification:

twophasekEpsilonCoeffs
    {
        nutMax           0.59;  // nutMax/(u_tau H)
    }

The two phase properties in the file constant/twophaseRASProperties require the following modification:

Tpsmall         Tpsmall [1 -3 -1 0 0 0 0] 3.4e-9; // Tpsmall H/(rhob u_tau)
Control

The simulation time control properties in the file system/controlDict require the following modifications:

endTime         45; // tend u_tau / H

deltaT          6e-5; 

writeInterval   3;
Postprocessing using fluidfoam

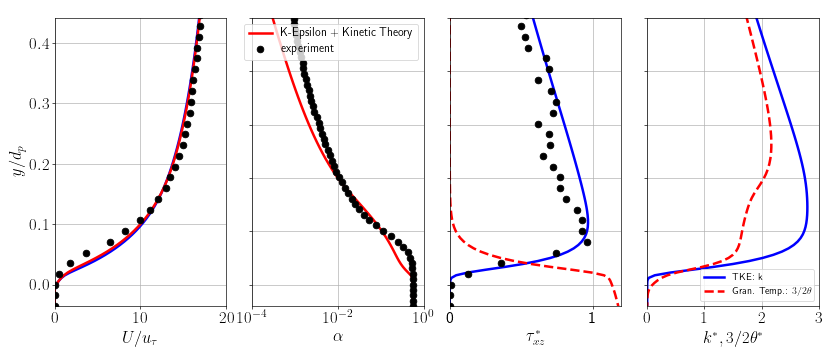
You just have to run the python script python plot_nd_tuto1DSheetFlow.py located in the folder tutorials/Py:

python plot_nd_tuto1DSheetFlow.py

and you should see the following figure:

Image
Figure 6: Comparison of two-phase numerical results with experiments of Revil-Baudard et al. (2015) in terms of velocity profiles, volume fraction, Reynolds shear stress and TKE/granular temperature using the kinetic theory with the k-epsilon turbulence model.

nd3DChannel560: Turbulent channel flow laden with particles

The LES tutorial - 3DChannel560: Turbulent channel flow laden with particles is found in the folder sedFoamDirectory/tutorials/3DChannel560. The following modifications need to be made in the tutorial input files in order to obtain a non-dimensional solution:

Mesh generation

The blockMeshDict in the folder system requires the following modification:

scale 1.0;
Boundary and initial conditions

The files 0_org/flma.a, 0_org/flmb.b, 0_org/fmma.a and 0_org/fmmb.b require the following modification:

internalField   uniform 127.551; // f/u_tau^4

The files 0_org/U.a and 0_org/U.b require the following modification:

scalar Ubar = 18.2;  // Ubar/u_tau
scalar h = 1.0;    // h/H
scalar retau = 560;
Physical properties

The physical properties in the file constant/transportProperties require the following modifications:

phasea
{
    rho             rho [ 1 -3 0 0 0 ] 2.6; // rho*
    nu              nu [ 0 2 -1 0 0 ] 0.0017857; // 1/Re_tau
    d               d [ 0 1 0 0 0 0 0 ] 0.00975; // d*
}

phaseb
{
    rho             rho [ 1 -3 0 0 0 ] 1.0; // rhob/rhob
    nu              nu [ 0 2 -1 0 0 ] 0.0017857; // 1/Re_tau
    d               d [ 0 1 0 0 0 0 0 ] 0.00975; // d*
}

nu              nu [ 0 2 -1 0 0 0 0 ] 0.0017857; // 1/Re_tau

nuMax           nuMax [0 2 -1 0 0 0 0] 1.7857e5; // nuMax/(u_tau H)

The gravity properties in the file constant/g require the following modification:

value           ( 0 -250.255 0 ); // -1/Fr^2

The kinetic theory properties in the file constant/kineticTheoryProperties require the following modification:

MaxTheta       MaxTheta [ 0 2 -2 0 0 0 0 ] 6377.55; // MaxTheta/u_tau^2

The permanent particle contact properties in the file constant/ppProperties require the following modification:

Fr               Fr [ 1 -1 -2 0 0 0 0 ] 0.0638;  // C_Fr/(rhob u_tau^2)

The turbulence model properties in both constant/turbulenceProperties.a and constant/turbulenceProperties.b files require the following modification:

LES{

     nutbMax         0.1785; // nutbMax/(u_tau H)
}
Control

The simulation time control properties in the file system/controlDict require the following modifications:

endTime         11;   // tend u_tau / H (turbulence initialization run)
//endTime         22;  // tend u_tau / H (final run)

deltaT          2.5e-4; 

writeInterval   0.7;
Running the simulation

As in the original 3DChannel560 tutorial you can launch the computation by executing Allrun for turbulence initialization. Once the end time has been modified and favreAveraging keyword set to true, you can launch the computation of time average variables by executing AllrunAverage.

Postprocessing using fluidfoam

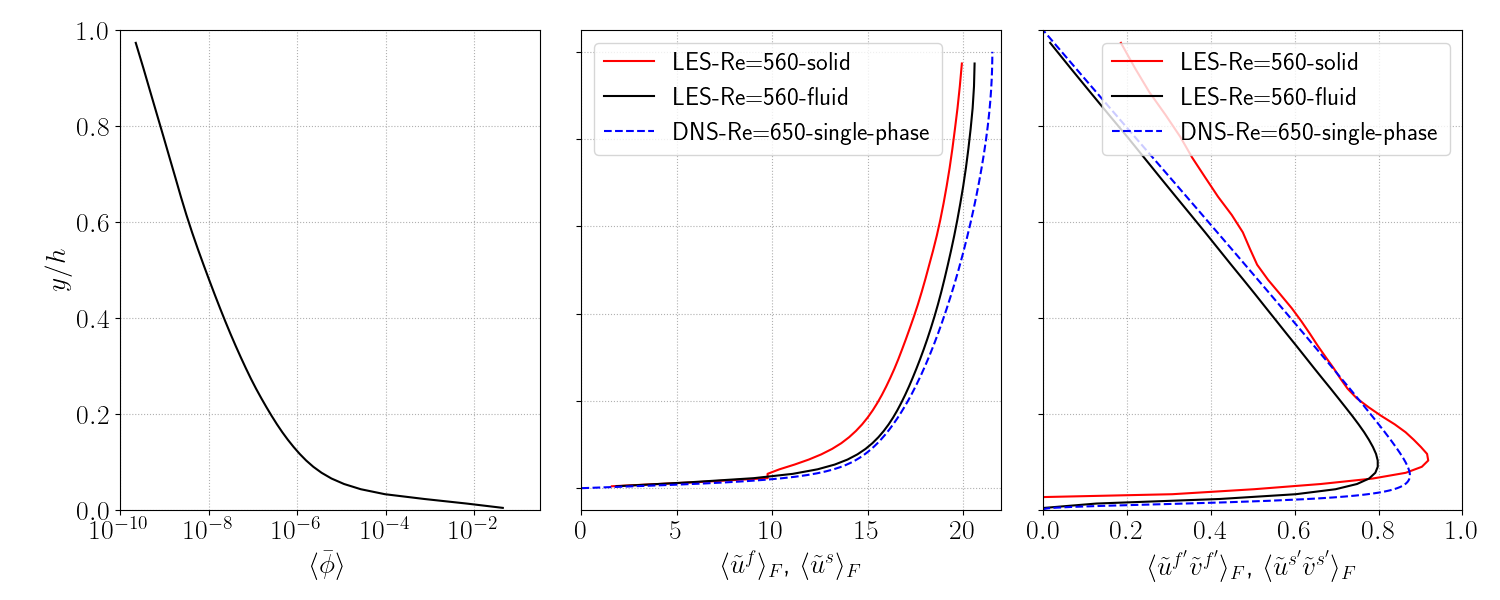
The post-processing python scripts writedata_nd_tuto3DChannel560.py and plot_nd_tuto3DChannel560.py are located in the folder tutorials/Py. To run this script, the latest output ( $t^*=22$ ) should be reconstructed. The script writedata_nd_tuto3DChannel560.py reads time averaged OpenFoam data, performs a spatial averaging operation and stores the 1D vertical profiles in a netCDF file located in the postProcessing directory of the case.

The script plot_nd_tuto3DChannel560.py reads the netCDF file and plots vertical profile of concentration, velocities and Reynolds stresses.

Image
Figure 2: Concentration, velocity and Reynolds stress profiles for the 3DChannel560 tutorial. The single phase turbulent channel flow profiles at Re=650 from the DNS database of K. Iwamoto, Y. Suzuki and N. Kasagi (2002) are also shown as a reference.