Reynolds-averaged flow tutorials
In this chapter multi-dimensional test cases are presented to illustrate the full SedFoam capabilities to deal with complex geometries as well as to provide configuration files to allow for the development of new configurations.
1DBoundaryLayer: Single-phase turbulent boundary layer flow
In this test case, tturbulence model k-omega (Wilcox, 1988) is validated for a single-phase boundary layer flow over a smooth surface. The numerical results are compared with the DNS results of Moser et al. (1999). A water column of dimensionless height is moving over a flat plate driven by a pressure gradient imposed along the x-axis. In this configuation, there are no sediments and the volumetric concentration of particles is set to alpha=0. A sketch of the 1D vertical computational domain is presented below:
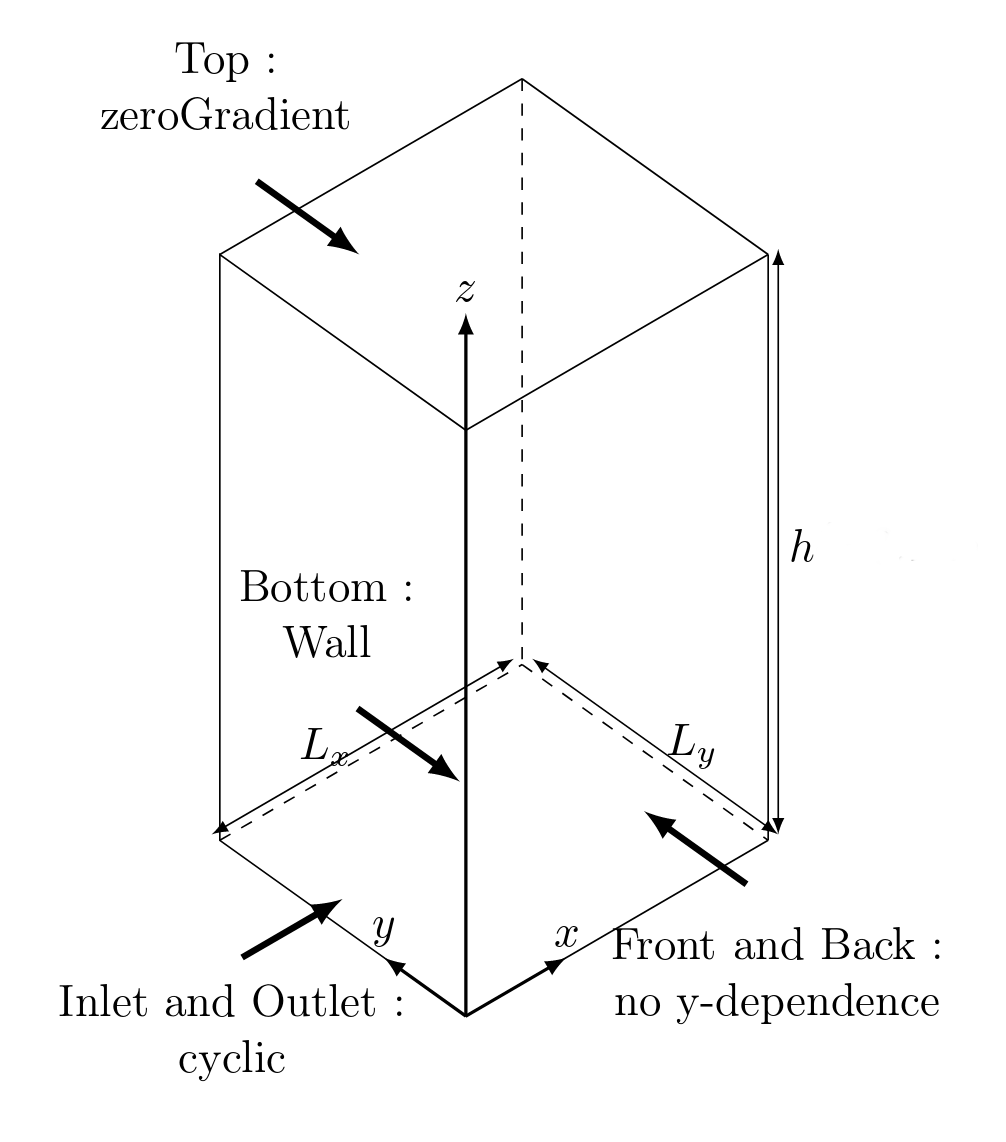
This tutorial is distributed with sedFoam under the folder sedFoamDirectory/tutorials/RAS/1DBoundaryLayer.
The domain is divided in 64 elements, with a cell expansion ratio of 1.026 along the vertical direction (the ratio between the first cell and the last cell is equal to 10). For such mesh the normalized distance to the wall from the first cell is with the bottom friction velocity and the fluid viscosity.
The physical properties are chosen to obtain a dimensionless solution with , . The parameters are set in the file constant/transportProperties and ar given as follows:
// * * * * * * * * * * * * sediment properties * * * * * * * * * * * * //
phasea
{
rho rho [ 1 -3 0 0 0 ] 1;
nu nu [ 0 2 -1 0 0 ] 0e0;
d d [ 0 1 0 0 0 0 0 ] 1.e-7;
sF sF [ 0 0 0 0 0 0 0 ] 1;
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65;
}
phaseb
{
rho rho [ 1 -3 0 0 0 ] 1;
nu nu [ 0 2 -1 0 0 ] 7.2727e-5;
d d [ 0 1 0 0 0 0 0 ] 3.e-3;
sF sF [ 0 0 0 0 0 0 0 ] 0.5;
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65;
}
d [ 0 1 0 0 0 0 0 ] 1;
}
//*********************************************************************** //
The boundary Reynolds number based on the friction velocity in Moser et al. (1999) is, . In sedFoam the flow is driven by a pressure gradient acting as a source term in the momentum equations. The pressure gradient is calculated by integrating the fluid momentum equation along th wall-normal direction sas follows:
and written in the file constant/forceProperties using the keyword gradPMEAN.
Boundary conditions
The inlet and outlet boundaries are set to cyclic while the front and back boundaries are set to empty. The latter boundary condition means that the y-components are not considered by the solver (i.e. 2 velocity components only). At the top boundary, the pressure is fixed to zero and a zero gradient (*i.e* Neumann boundary condition) is imposed on all the other quantities. At the wall, the velocity is set to zero, a zeroGradient condition is imposed for the pressure and a wall function is imposed for the TKE dissipation.
The wall function is prescribing the value of TKE dissipation at the wall to follow the analytical solution from Wilcox (1988). In this tutorial, a rough wall function is used prescribing the value of at the wall following:
with a tuning parameter taking into account bed roughness as follows:
Post-processing using python
The SedFoam results are plotted using the python script plot_tuto1DBoundayLayer.py located in the folder tutorials/Py:
python plot_tuto1DBoundaryLayer.py
and you should see the following figure:
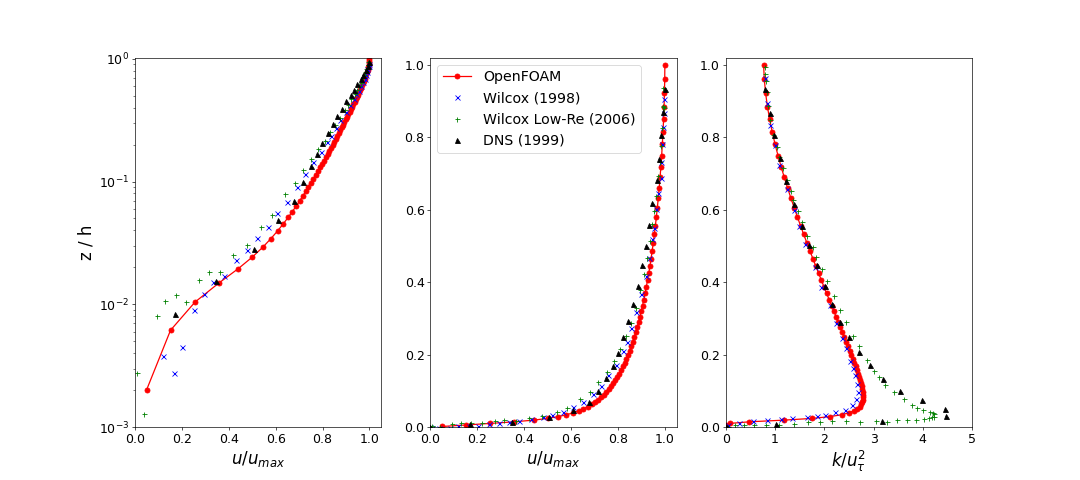
Moser, R. D., Kim, J., and Mansour, N. N. (1999). Direct numerical simulation of turbulent channel flow up to retau=590. Physics of Fluids, 11(4):943-945. Wilcox, D. C. (2008). Formulation of the k-w turbulence model revisited. AIAA Journal, 46(11):2823–2838.
1DBedloadTurb: Turbulent bedload transport
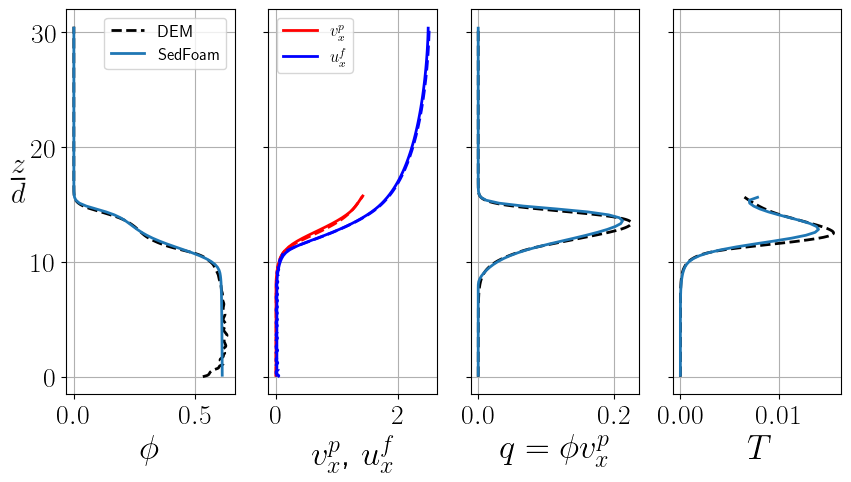
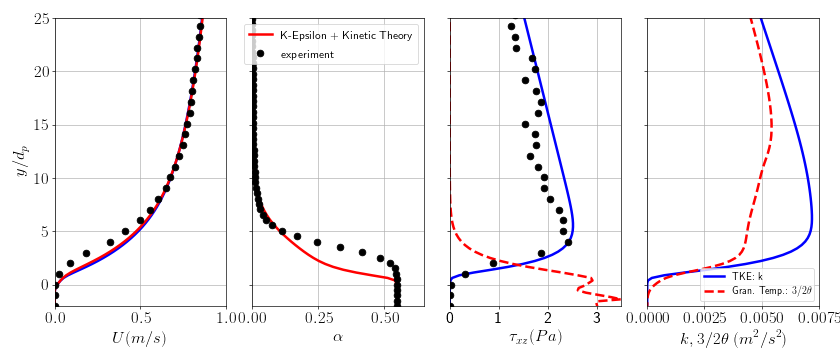
The aim of this tutorial is to explain how to use the kinetic theory to model the sediment phase in turbulent bedload transport. It is based on a comparison coupled fluid-DEM (discrete element method) simulations. In DEM simulations, the motion of each particles is solved individually. The source code is YADE (Smilauer et al. 2015) and the coupling with the fluid phase presented in Maurin et al. (2015). The exact same fluid model is considered in both the fluid-DEM simulations and in the sedfoam simulation (mixing length) in order to focus on the granular flow modelling. Averaged quantities are computed in the DEM (volume fraction, particle velocity, granular temperature, etc.) which will be considered as a basis to compare with the sedFoam simulation. A complete description and analyses of the granular flow modeling with the kinetic theory can be found Chassagne et al. (2023).

Pre-processing
This tutorial is distributed with SedFoam under the folder sedFoamDirectory/tutorials/RAS/1DBedLoadTurb.
Mesh generation
The numerical domain consists of a square of side length L = 0.00147 m in the x-y plane and of height h=0.147 m in the vertical direction z. The side length is chosen to ensure a unity cell aspect ratio. A uniform mesh of 1 by 1 by 120 cells will be used. The block structure is the same as for the Sedimentation test case.
The mesh is generated by running blockMesh from within the case directory:
blockMesh
Boundary and initial conditions
The case is set up to start at time s, again the initial field data are stored in a 0_org sub-directory of the case directory. The 0_org sub-directory contains several files: alpha.a, alphaMinFriction, alphaPlastic, U.a, U.b, p_rbgh, pa, Theta, one for each of the solid phase volume fraction (alpha.a), velocities of solid and fluid phases (U.a and U.b), the reduced pressure (p_rbgh) fields whose initial values and boundary conditions must be set. The initial profile of concentration (in alpha.a) is a hyperbolic tangent whose parameters have been compute so that the exact same amount of granular mass as in the DEM simulation is set in the sedFoam simulation. Compared with the sedimentation test case, no-slip boundary conditions are imposed for both phase velocity at the top and bottom boundaries.
forAll(mesh.C(), i)
{
scalar y = mesh.C()[i].y();
alpha_a[i] = 0.305*(1.0+tanh((12.5*0.006-y)/0.005));
}
Physical properties
The transportProperties file for the 1DBedloadTurb case is shown below. The same particle properties as in the DEM are.
// * * * * * * * * * * * * sediment properties * * * * * * * * * * * * //
phasea
{
rho rho [ 1 -3 0 0 0 ] 2500;
nu nu [ 0 2 -1 0 0 ] 1e-6;
d d [ 0 1 0 0 0 0 0 ] 6.e-3;
sF sF [ 0 0 0 0 0 0 0 ] 1; // shape Factor to adjust settling velocity for non-spherical particles
hExp hExp [ 0 0 0 0 0 0 0 ] 3.1; // hindrance exponent for drag: beta^(-hExp) (2.65 by default)
}
// * * * * * * * * * * * * fluid properties * * * * * * * * * * * * //
phaseb
{
rho rho [ 1 -3 0 0 0 ] 1000;
nu nu [ 0 2 -1 0 0 ] 1.e-6;
d d [ 0 1 0 0 0 0 0 ] 3.e-3;
sF sF [ 0 0 0 0 0 0 0 ] 0.5;
hExp hExp [ 0 0 0 0 0 0 0 ] 3.1;
}
//*********************************************************************** //
transportModel Newtonian;
nu nu [ 0 2 -1 0 0 0 0 ] 1.e-6;
nuMax nuMax [0 2 -1 0 0 0 0] 1e2; // viscosity limiter for the Frictional model (required for stability)
alphaSmall alphaSmall [ 0 0 0 0 0 0 0 ] 1e-5; // minimum volume fraction (phase a) for division by alpha
// ************************************************************************* //
The fluid and particles are submitted to gravity. This is accounted for as a pressure gradient source term in the momentum conservation equations. It corresponds to gradPMEAN in file forceProperties with , with (kg/s), (m/s^2) and . The tilt parameter is set to 1, so that the source term in the granular momentum equation is automatically set to .
// * * * * * * * * * * * * * following are for presure * * * * * * * * * * * * * * * // gradPMEAN gradPMEAN [ 1 -2 -2 0 0 0 0 ] (490.5 0 0 ); // mean pressure tilt tilt [ 0 0 0 0 0 0 0 ] 1; // To impose same gravity term to both phases Cvm Cvm [ 0 0 0 0 0 ] 0; // Virtual/Added Mass coefficient Cl Cl [ 0 0 0 0 0 ] 0; // Lift force coefficient Ct Ct [ 0 0 0 0 0 ] 0; // Eddy diffusivity coefficient for phase a debugInfo true; writeTau true; // * * * * * * * * * * * * end of definition of pressure * * * * * * * * * * * * * //
The fluid turbulence is modelled with a mixing length approach with the same parameters as in the DEM fluid model (expoLM=1, kappaLM=0.41, alphaMaxLM=0.61) :
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //
simulationType RAS;
RAS{
RASModel twophaseMixingLength;
//RASModel twophasekEpsilon;
//RASModel twophasekOmega;
turbulence on;
printCoeffs on;
twophaseMixingLengthCoeffs
{
expoLM 1.0;
alphaMaxLM 0.61;
kappaLM 0.41;
}
}
// ************************************************************************* //
In the dictionary interfacialProperties file the drag model from DallaValle is used (as in the DEM).
Kinetic theory will be used to compute the kinetic contributions of granular stresses. Be sure to set granularRheology to off in granularRheologyProperties. The kineticTheoryProperties file contains all information to set up thze kinetic theory model. First, particle properties have to be given, restitution coefficient and interparticle friction . alphaMax is the maximum packing fraction and phi is the angle of repose, below which the granular flow stops moving. This angle depends on the interparticle friction and an empirical formula to compute phi is given in Chassagne et al. (2023) (Appendix). killJ2_, allows to account for (0) or neglect (1) any transfer of fluctuating energy from the fluid to the particles. quadraticCorrectionJ1_ allows you to account for (1) or neglect (0) additional dissipation of granular temperature by the drag force, due to the quadratic nature of drag force in turbulent flows. Then you have to choose which model to use for each of the coefficient of the kinetic theory. The models used in this tutorial correspond to the model developed in Chassagne et al. (2023). The Garzo and Dufty (1999) coefficients are used for the viscosity, conductivity and pressure coefficient. The pressure coefficient of Lun et al. (1984) is the same as the one of Garzo and Dufty (1999). A saltation model can be specified (none by default). This modifies the viscosity and conductivity coefficients in the dilute part of the granular flow to account for saltation motions. In the current version of the code, only the GarzoDufty models can be coupled with a saltation model. The Chialvo & Sundaresan (2013) radial distribution function is used, and it is the only one that accounts for the effect of the interparticle friction coefficient (Chassagne et al. (2013)).
// * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // kineticTheory on; limitProduction off; extended off; e e [ 0 0 0 0 0 0 0 ] 0.7; muPart muPart [ 0 0 0 0 0 0 0 ] 0.4; alphaMax alphaMax [ 0 0 0 0 0 0 0 ] 0.635; MaxTheta MaxTheta [ 0 2 -2 0 0 0 0 ] 0.5; phi phi [ 0 0 0 0 0 0 0 ] 20.487; //mus = 0.35 = sin(phi*pi/180) psi psi [ 0 0 0 0 0 0 0 ] 0.0; killJ2_ killJ2_ [ 0 0 0 0 0 0 0] 1; quadraticCorrectionJ1_ quadraticCorrectionJ1_ [ 0 0 0 0 0 0 0 ] 1; viscosityModel GarzoDufty; conductivityModel GarzoDufty; granularPressureModel Lun; saltationModel Jenkins; radialModel ChialvoSundaresan; // ************************************************************************* //
Discretisation and linear-solver settings
The numerical schemes and the solvers are the same as in the 1DSedim case.
Control
The system/controlDict file is shown thereafter. The endTime is fixed to 30 s with an output every 5s with an adjustable time step limited to 5e-3 s. The simulation should last around 20 minutes.
application sedFoam; startFrom latestTime; startTime 0; stopAt endTime; endTime 30; deltaT 1e-5; writeControl adjustableRunTime; writeInterval 1; purgeWrite 0; writeFormat ascii; writePrecision 6; timeFormat general; timePrecision 6; runTimeModifiable on; adjustTimeStep on; maxCo 0.1; maxAlphaCo 0.1; maxDeltaT 1e-3;
Post-processing using python
You just have to run the python script plot_tuto1DBedLoadTurb.py located in the folder tutorials/Py:
python plot_tuto1DBedLoadTurb.py
and you should see the following figures:
1DSheetFlow: Turbulent sheet-flows
In this tutorial, the turbulent flow over a flat erodible bed drives sediment transport in the intense turbulent bedload tranpsort regime usually referred to as sheet-flow. The results are compared with experimental data from Revil-Baudard et al. (2015). Light-weight non-spherical PMMA particles of median diameter d=3 mm are used having a settling velocity in quiescent water of about m/s. The averaged flow velocity is about U=0.52 m/s corresponding to a bed friction velocity of m/s and a dimensionless bed shear stress, the so-called Shields number , equal to 0.44.

Pre-processing
This tutorial is distributed with sedFoam under the folder sedFoamDirectory/tutorials/RAS/1DSheetFlow.
Mesh generation
The numerical domain consists of a square of side length L = 0.00085 m in the x-y plane and of height h=0.17 m in the vertical direction z. The side length is chosen to ensure a unity cell aspect ratio. A uniform mesh of 1 by 1 by 400 cells will be used. The block structure is the same as for the Sedimentation test case.
The mesh is generated by running blockMesh from within the case directory:
blockMesh
Boundary and initial conditions
The case is set up to start at time t = 0 s, again the initial field data are stored in a 0_org sub-directory of the case directory. The 0_org sub-directory contains several files: alpha.a, alphaMinFriction, alphaPlastic, U.a, U.b, p_rbgh, muI, pa, pa_new, Theta, k.b, epsilon.b, omega.b and nut one for each of the solid phase volume fraction (alpha.a), velocities of solid and fluid phases (U.a and U.b), the reduced pressure (p_rbgh) fields whose initial values and boundary conditions must be set. No-slip boundary conditions are imposed at the bottom and zero gradient at the top for both phase velocities.
Physical properties
The transportProperties file for the 1DSheetFlow case is shown below:
phasea
{
rho rho [ 1 -3 0 0 0 ] 1190;
nu nu [ 0 2 -1 0 0 ] 0e0;
d d [ 0 1 0 0 0 0 0 ] 3.e-3;
sF sF [ 0 0 0 0 0 0 0 ] 0.5; // shape Factor to adjust settling velocity for non-spherical particles
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65; // hindrance exponent for drag: beta^(-hExp) (2.65 by default)
}
phaseb
{
rho rho [ 1 -3 0 0 0 ] 1000;
nu nu [ 0 2 -1 0 0 ] 1.e-6;
d d [ 0 1 0 0 0 0 0 ] 3.e-3;
sF sF [ 0 0 0 0 0 0 0 ] 0.5;
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65;
}
//*********************************************************************** //
transportModel Newtonian;
nu nu [ 0 2 -1 0 0 0 0 ] 1.e-6;
nuMax nuMax [0 2 -1 0 0 0 0] 1e-1; // viscosity limiter for the Frictional model (required for stability)
alphaSmall alphaSmall [ 0 0 0 0 0 0 0 ] 1e-6; // minimum volume fraction (phase a) for division by alpha
alphaAlpha alphaAlpha [ 0 0 0 0 0 ] 0; // surface tensionThe physical property of the particles (diameter and density) and of the fluid (density and kinematic viscosity) have been set to the experimental values from Revil-Baudard et al. (2015).
Revil-Baudard, T., Chauchat, J., Hurther, D., and Barraud, P.-A. (2015). In- vestigation of sheet-flow processes based on novel acoustic high-resolution velocity and concentration measurements. Journal of Fluid Mechanics, 767:1–30.
In the dictionary interfacialProperties file the drag model from GidaspowSchillerNaumann is used and the shape factor sF is taken to 0.5 to match the settling velocity of a single particle with the measured data (w_fall = 0.056 m/s).
In this tutorial, the kinetic theory is used for the granular stress model and the kineticTheoryProperties reads:
kineticTheory on; equilibrium off; limitProduction off; e e [ 0 0 0 0 0 0 0 ] 0.8; alphaMax alphaMax [ 0 0 0 0 0 0 0 ] 0.6; DiluteCut DiluteCut [ 0 0 0 0 0 0 0 ] 0.00000; ttzero ttzero [ 0 0 1 0 0 0 0 ] 0; ttone ttone [ 0 0 1 0 0 0 0 ] 0; MaxTheta MaxTheta [ 0 2 -2 0 0 0 0 ] 0.5; phi phi [ 0 0 0 0 0 0 0 ] 32.0; psi psi [ 0 0 0 0 0 0 0 ] 0.0; KineticJ1 KineticJ1 [ 0 0 0 0 0 0 0 ] 1; //turn off the viscous dissipation KineticJ2 KineticJ2 [ 0 0 0 0 0 0 0] 0; KineticJ3 KineticJ3 [ 0 0 0 0 0 0 0] 0; viscosityModel Syamlal; conductivityModel Syamlal; granularPressureModel Lun; frictionalStressModel SrivastavaSundaresan; radialModel CarnahanStarling;
The turbulence model is set to kEpsilon in turbulenceProperties:
simulationType RAS;
RAS{
RASModel twophasekEpsilon;
turbulence on;
printCoeffs on;
}Discretisation and linear-solver settings
The numerical schemes and the solvers are the same as in the 1DSedim case except that numerical schemes for the turbulent quantities (k, , ) have been added:
ddtSchemes
{
default Euler implicit;
}
gradSchemes
{
default Gauss linear;
}
divSchemes
{
default none;
// alphaEqn
div(phi,alpha) Gauss limitedLinear01 1;
div(phir,alpha) Gauss limitedLinear01 1;
// UEqn
div(phi.a,U.a) Gauss limitedLinearV 1;
div(phi.b,U.b) Gauss limitedLinearV 1;
div(phiRa,Ua) Gauss limitedLinear 1;
div(phiRb,Ub) Gauss limitedLinear 1;
// pEqn
div(alpha,nu) Gauss linear;
// k and EpsilonEqn
div(phi.b,k.b) Gauss limitedLinear 1;
div(phi.b,epsilon.b) Gauss limitedLinear 1;
div(phi.b,omega.b) Gauss limitedLinear 1;
// ThetaEqn
div(phi,Theta) Gauss limitedLinear 1;
// alphaPlastic
div(phia,alphaPlastic) Gauss limitedLinear01 1;
// pa
div(phia,pa_new_value) Gauss limitedLinear 1;
}
laplacianSchemes
{
default none;
// UEqn
laplacian(nuEffa,U.a) Gauss linear corrected;
laplacian(nuEffb,U.b) Gauss linear corrected;
laplacian(nuFra,U.a) Gauss linear corrected;
// pEqn
laplacian((rho*(1|A(U))),p_rbgh) Gauss linear corrected;
// k and EpsilonEqn
laplacian(DkEff,k.b) Gauss linear corrected;
laplacian(DkEff,beta) Gauss linear corrected;
laplacian(DepsilonEff,epsilon.b) Gauss linear corrected;
laplacian(DepsilonEff,beta) Gauss linear corrected;
laplacian(DomegaEff,omega.b) Gauss linear corrected;
//ThetaEqn
laplacian(kappa,Theta) Gauss linear corrected;
laplacian(kappa2,alpha) Gauss linear corrected;
}
interpolationSchemes
{
default linear;
}
snGradSchemes
{
default corrected;
}
fluxRequired
{
default no;
p_rbgh ;
}
Control
The system/controlDict file is modified compared with the laminar bed load test case, the time step is reduced to s and the endTime is reduced to 150 s that is enough for the steady state to be reached.
application sedFoam; startFrom latestTime; startTime 0; stopAt endTime; endTime 150; deltaT 2e-4; writeControl adjustableRunTime; writeInterval 10; purgeWrite 0; writeFormat ascii; writePrecision 6; writeCompression uncompressed; timeFormat general; timePrecision 6; runTimeModifiable on; adjustTimeStep yes; maxCo 0.1; maxAlphaCo 0.1; maxDeltaT 5e-4;
Post-processing using python
You just have to run the python script plot_tuto1DSheetFlow.py located in the folder tutorials/Py:
python plot_tuto1DSheetFlow.py
and you should see the following figure:
2DPipelineScour: Scour around an horizontal cylinder
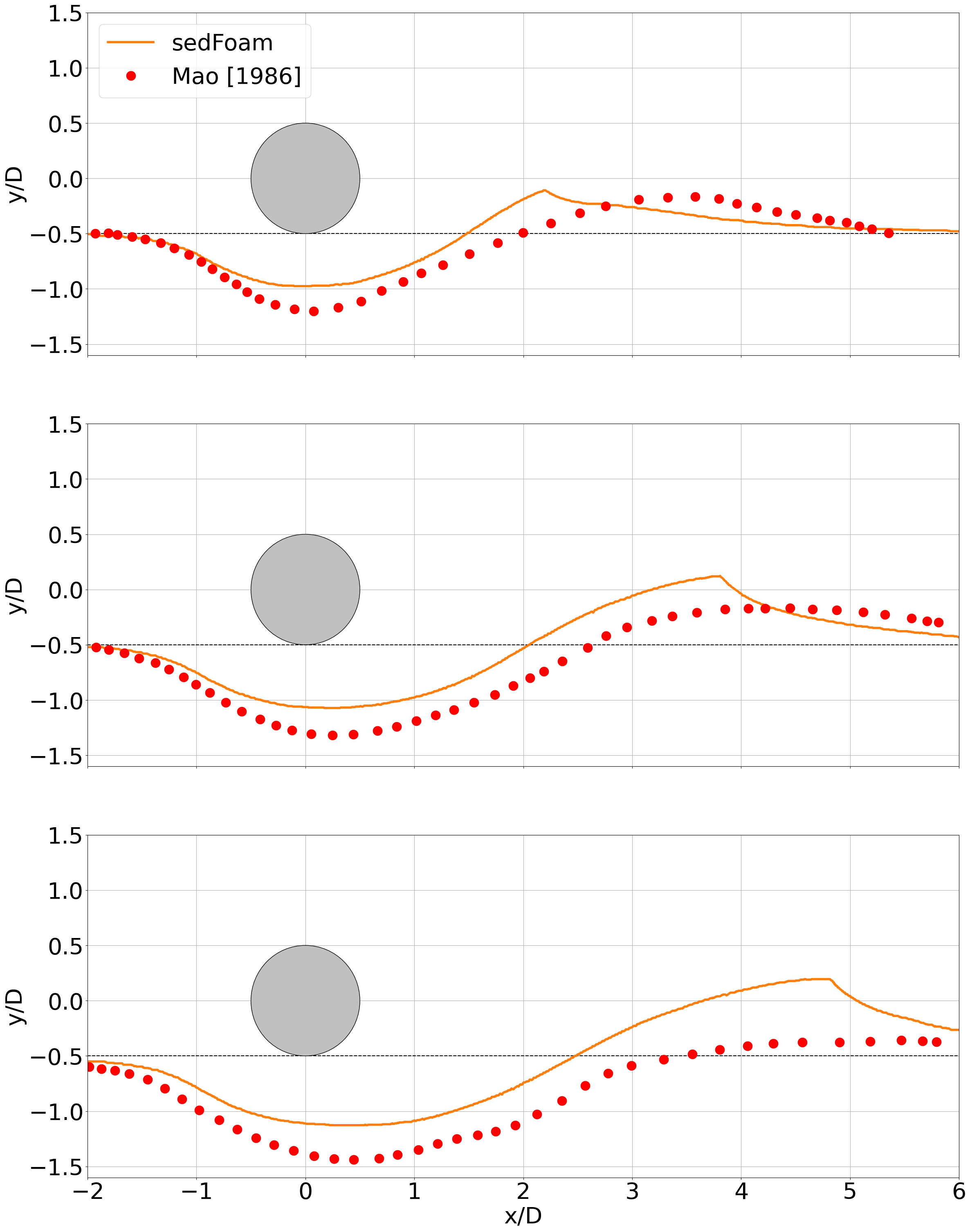
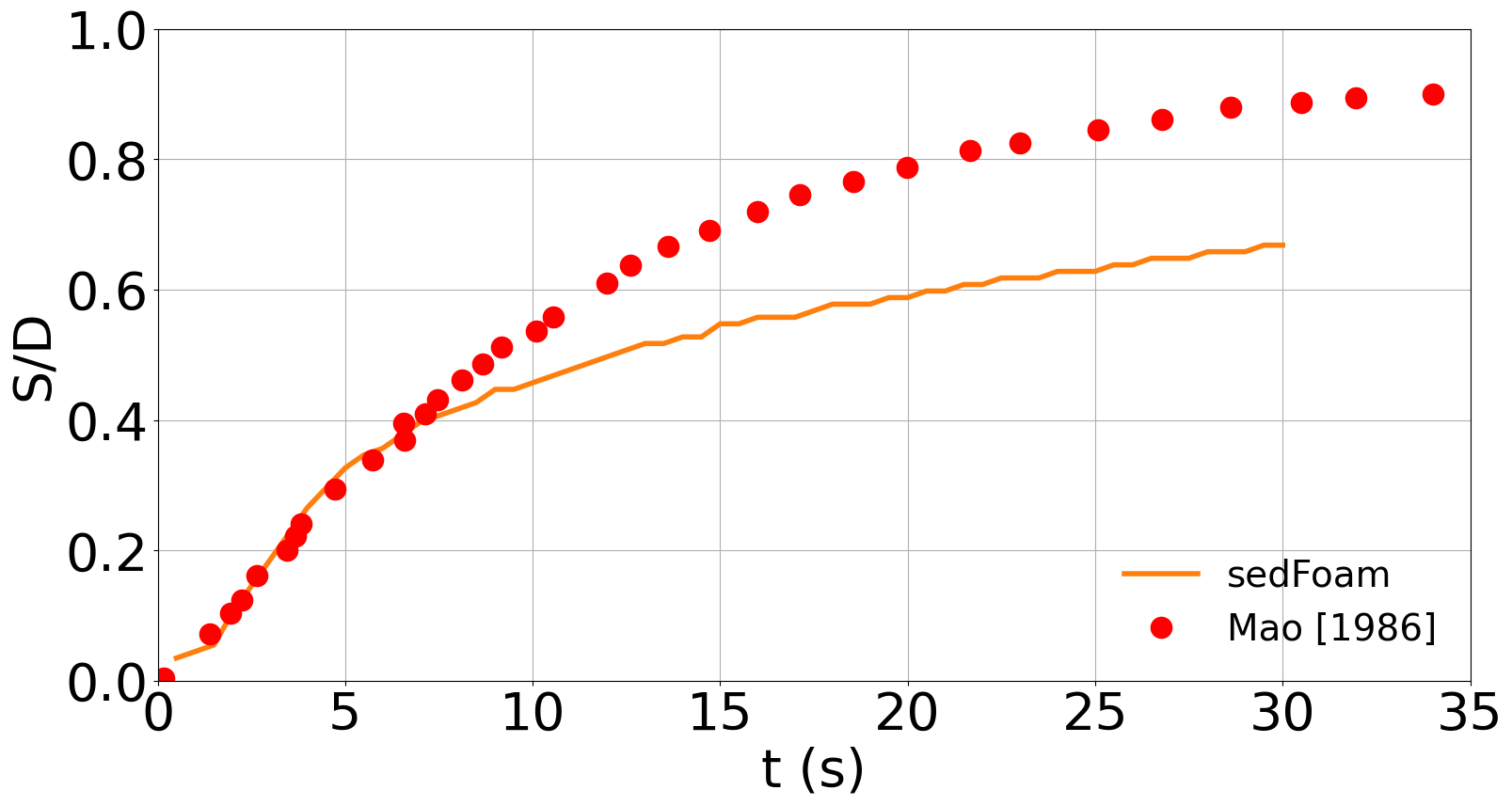
In this tutorial, the experimental configuration investigating scour under a submarine pipeline from Mao (1986) is reproduced numerically.
Pre-processing
This tutorial is distributed with SedFoam under the folder sedFoamDirectory/tutorials/RAS/2DPipelineScour.
Mesh generation
The numerical domain dimensions are presented in figure 7. A cylinder of diameter is placed 15 diameters away from the inlet. The overall domain dimensions were 35 diameters long and 6.1 diameters high. The mesh is generated using the OpenFOAM utilities blockMesh and snappyHexMesh. The mesh generated with blockMesh is a simple rectangle with regular grid spacing excepted in the vertical direction where cells are expanding toward the top boundary. The snappyHexMesh utility uses the file Cyl.stl located in the constant/triSurface directory containing the cylinder geometry to remove mesh cells inside it, add layers of cells around the cylinder and refine cells in regions of high concentration gradient at the bed.
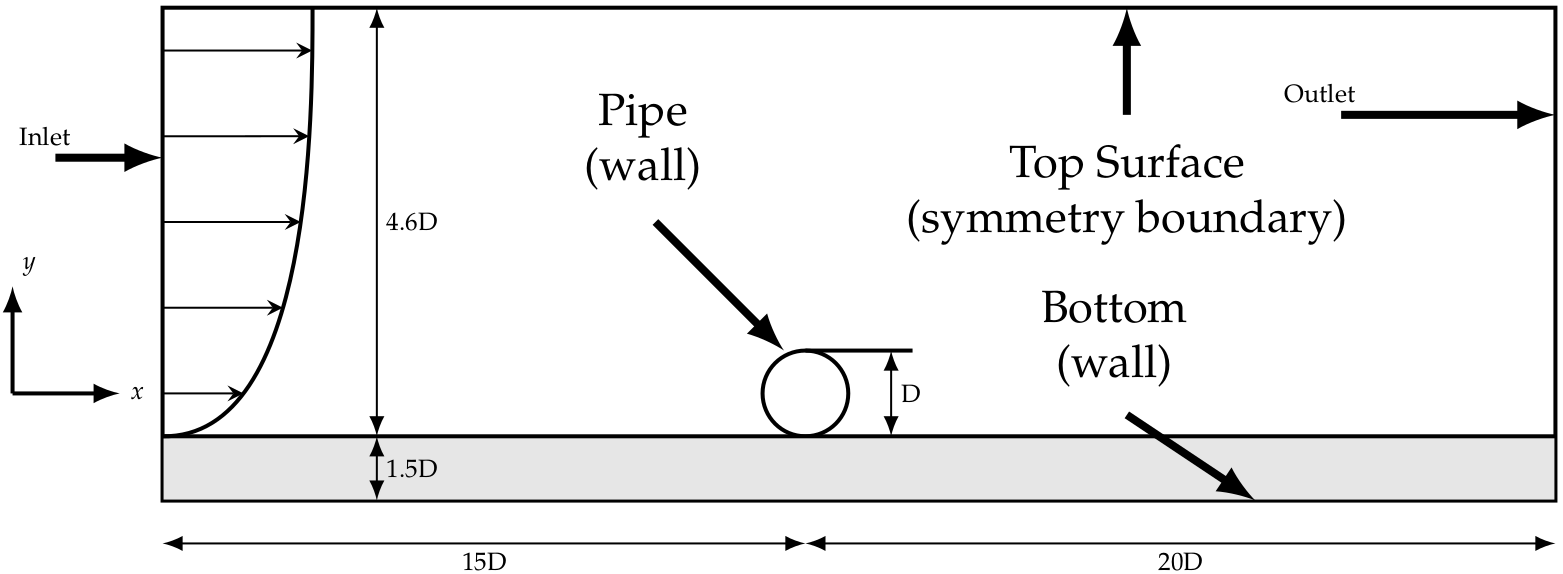
Depending on the turbulence model used, the number of layers should not be the same to accurately predict the boundary layer around the cylinder. The default snappyHexMeshDict in the system directory is written to perform simulations using the turbulence model. For simulations using the model, the user should use/rename the file snappyHexMeshDict_kEpsilon located in the system directory to generate the mesh.
Boundary and initial conditions
The case is set up to start at time t = 0 s, as for the previous tutorials the initial fields data are stored in the 0_org sub-directory of the case directory.
The top boundary condition is a symmetryPlane. The outlet pressure is set to 0. The outlet boundary condition for the velocity is inletOulet corresponding to a homogeneous Neumann boundary condition for outgoing flows and a homogeneous Dirichlet boundary condition for incoming flows. The inlet is decomposed into two parts. From the bottom to , a wall-type boundary condition is applied. From to the top, a rough wall log law velocity profile is used following the expression
with the bottom friction velocity, the von Karman constant and the Nikuradse roughness length. The velocity is increased linearly during the first 4 seconds of the simulation. Inlet values for turbulent quantities were set following , and with the bulk velocity, the distance from the bed to the top boundary and an empirical constant.
The sediment bed is initialised using the expression .
Physical properties
The transportProperties file for the 2DPipelineScour case is shown below:
phasea
{
rho rho [ 1 -3 0 0 0 ] 2650;
nu nu [ 0 2 -1 0 0 ] 1e-6;
d d [ 0 1 0 0 0 0 0 ] 0.36e-3;
sF sF [ 0 0 0 0 0 0 0 ] 1.; // shape Factor to adjust settling velocity for non-spherical particles
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65; // hindrance exponent for drag: beta^(-hExp) (2.65 by default)
}
phaseb
{
rho rho [ 1 -3 0 0 0 ] 1000;
nu nu [ 0 2 -1 0 0 ] 1.e-06;
d d [ 0 1 0 0 0 0 0 ] 10e-6;
sF sF [ 0 0 0 0 0 0 0 ] 1.;
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65;
}
//*********************************************************************** //
alphaSmall alphaSmall [ 0 0 0 0 0 0 0 ] 1e-4; // minimum volume fraction (phase a) for division by alpha
alphaAlpha alphaAlpha [ 0 0 0 0 0 ] 0; // surface tension
Cvm Cvm [ 0 0 0 0 0 ] 0; // Virtual/Added Mass coefficient
Cl Cl [ 0 0 0 0 0 ] 0; // Lift force coefficient
transportModel Newtonian;
nu nu [ 0 2 -1 0 0 0 0 ] 1e-06;
nuMax nuMax [0 2 -1 0 0 0 0] 10; // viscosity limiter for the Frictional model (required for stability)
The physical property of the particles (diameter and density) and of the fluid (density and kinematic viscosity) have been set to the values given in Mao (1986).
Control
The system/controlDict file indicates that for this case the time step is adaptative to have a maximum Courant number (maxCo) below 0.1 and that the computation ends at 45s of dynamics.
application sedFoam; startFrom latestTime; startTime 0; stopAt endTime; endTime 45; deltaT 1.e-4; writeControl adjustableRunTime; writeInterval 0.5; purgeWrite 0; writeFormat binary; writePrecision 6; writeCompression false; timeFormat general; timePrecision 6; runTimeModifiable on; adjustTimeStep yes; maxCo 0.1; maxAlphaCo 0.3; maxDeltaT 15.e-5;
Computation launching
As for the previous case, you can launch the computation by executing * Allrun *. The simulations is run in parallel on 16 cores.
Post-processing using python
The post-processing python scripts plot_profiles2DPipelineScour.py and plot_depth2DPipelineScour.py are located in the folder tutorials/Py.
The script _profiles2DPipelineScour.py plots bed profiles at 11s, 18s and 25s compared with experimental data like in the following figure:
The script plot_depth2DPipelineScour.py plots the maximum scour depth compared with experimental data like in the following figure:
3DScourCylinder: Scour around a vertical cylinder
In this tutorial, the experimental configuration from Roulund et al (2005) is reproduced numerically.
Pre-processing
This tutorial is distributed with SedFoam under the folder sedFoamDirectory/tutorials/RAS/3DScour.
A 1D boundary layer simulation needs to be run (see folder 1D and Allrun.pre) for fore information. The result of this simulations is then used to intialize the 3D configuation and to impose the inlet boundary condition.
Mesh generation
The numerical domain dimensions are presented in figure 10. A cylinder of diameter is placed 4 diameters away from the inlet. The overall domain dimensions were 13 diameters long, 8 diameters wide and 2 diameters high. The mesh is generated using the OpenFOAM utilities blockMesh and a perl script is used to create the blockMeshDict. A sediment bed layer having a thickness of D/4 is initially set-up except around the cylinder where a scour pit is created with a thickness D and a radius of 2D. The sediments are made of medium sand with median diameter d =0.26 mm and density , the corresponding fall velocity of an individual grain in quiescent water is . The Shields parameter at the inlet and the Reynolds number are the same as is in Roulund et al. (2005), and , respectively. For the sand layer, outside the scour pit, the mesh is composed of 100 vertical levels having a geometric distribution with a common ratio . In the scour pit, an additional 100 grid points are used with a geometric common ratio .
The mesh is generated using the perl script 'generateMeshDict_cyl_3dsedim.pl' using the folowing command:
perl generateMeshDict_cyl_3dsedim.pl 0.4 -0.025 0.0 0.2 -0.1 0.4 1.2 0.8
See the perl script for details about the different parameters.
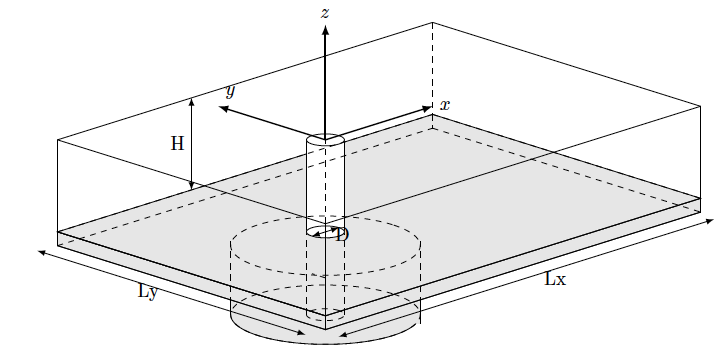
Boundary and initial conditions
The boundary conditions have to be adapted from the RB case :
(i) At the inlet, vertical profiles obtained from a 1D vertical simulation are imposed for . Zero transverse velocity is prescribed.
(ii) At the outlet, Neumann boundary conditions are specified for all quantities, except for the pressure for which a homogeneous Dirichlet boundary condition is imposed for the reduced pressure. For the velocities, a homogeneous Neumann boundary condition is used when the velocity vector points outside of the domain at the outlet, and a homogeneous Dirichlet boundary condition is used otherwise.
(iii) At the top and side boundaries, the same boundary conditions as in the Rigid-Bed case are used.
(iv) At the walls (including the cylinder), zero velocity (no-slip) is imposed for the three components and a small value is imposed for the turbulent kinetic energy (TKE) k.b. The boundary condition for is specified using the classical wall function from openFOAM at the cylinder and using a constant value is imposed at the bottom.
Physical properties
The following variables are considered to reproduce the experimental results of Pailha et al. (2008):
| Properties | Value |
|---|---|
| Solid density | |
| Fluid density | |
| Fluid viscosity | |
| Mean particle diameter |
The transportProperties file for the 3DScour case is shown below:
phasea
{
rho rho [ 1 -3 0 0 0 ] 2650;
nu nu [ 0 2 -1 0 0 ] 1e-6;
d d [ 0 1 0 0 0 0 0 ] 0.26e-3;
sF sF [ 0 0 0 0 0 0 0 ] 1.; // shape Factor to adjust settling velocity for non-spherical particles
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65; // hindrance exponent for drag: beta^(-hExp) (2.65 by default)
}
phaseb
{
rho rho [ 1 -3 0 0 0 ] 1000;
nu nu [ 0 2 -1 0 0 ] 1.e-06;
d d [ 0 1 0 0 0 0 0 ] 10e-6;
sF sF [ 0 0 0 0 0 0 0 ] 1.;
hExp hExp [ 0 0 0 0 0 0 0 ] 2.65;
}
alphaSmall alphaSmall [ 0 0 0 0 0 0 0 ] 1e-6; // minimum volume fraction (phase a) for division by alpha
alphaAlpha alphaAlpha [ 0 0 0 0 0 ] 0; // surface tension
Usmall Usmall [ 0 1 -1 0 0 0 0 ] 1.0e-10; // minimum friction velocity for local Schmidt calculation
Ufall Ufall [ 0 1 -1 0 0 0 0 ] 3.44e-2; //sediment fall velocity
transportModel Newtonian;
nu nu [ 0 2 -1 0 0 0 0 ] 1e-06;
nuMax nuMax [0 2 -1 0 0 0 0] 100; // viscosity limiter for the Frictional model (required for stability)
The physical property of the particles (diameter and density) and of the fluid (density and kinematic viscosity) have been set to the values given in Roulund et al (2005).
Rheological parameters
The granular stress model is set to granularRheology using the following parameters:
granularRheology on; granularDilatancy off; granularCohesion off; alphaMaxG alphaMaxG [ 0 0 0 0 0 0 0 ] 0.625; mus mus [ 0 0 0 0 0 0 0 ] 0.63; mu2 mu2 [ 0 0 0 0 0 0 0 ] 1.13; I0 I0 [ 0 0 0 0 0 0 0 ] 0.6; Bphi Bphi [ 0 0 0 0 0 0 0 ] 0.66; n n [ 0 0 0 0 0 0 0 ] 2.5; Dsmall Dsmall [ 0 0 -1 0 0 0 0 ] 1e-4; relaxPa relaxPa [ 0 0 0 0 0 0 0 ] 3e-4; zbed zbed [ 0 1 0 0 0 0 0 ] 0.0; FrictionModel MuI; PPressureModel MuI; FluidViscosityModel BoyerEtAl;
Control
The system/controlDict file indicates that for this case the time step is adaptative to have a maximum Courant number (maxCo) below 0.5.
Computation launching
As for the previous case, you can launch the computation by executing * Allrun *. The mesh is quite large and at least 100 cores are needed to perform this simulation.
Post-processing using paraview
The post-processing is mostly performed using paraview. No python script is provided withthi configuration at the moment.
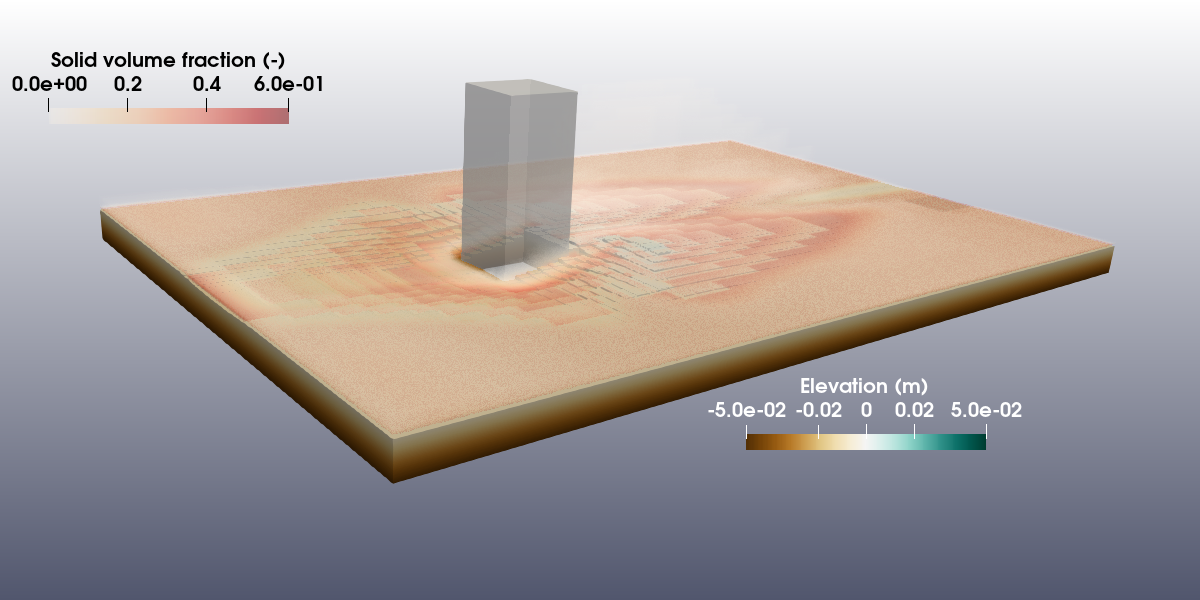
3DScourSqr: Scour around a vertical square cylinder
In this tutorial, the hybrid RANS-LES k-omega 2006 SAS is applied to the live-bed configuration of scour around a vertical square cylinder.
Pre-processing
This tutorial is distributed with SedFoam under the folder sedFoamDirectory/tutorials/RAS/3DScourSqr.
Similarly as the 3DScour configuration, a 1D boundary layer simulation needs to be run and then used to intialize the 3D configuation and to impose the inlet boundary condition.
Mesh generation
A square-based cylinder and side is placed 4D away from the inlet. Numerical simulations have been performed with the following computational domain : 12D long, 8D wide and 2,5D high. The mesh is generated using the OpenFOAM utilities blockMesh with Lu, Ld and H the upstream, downstream, width length of the computational domain. A sediment bed layer having a thickness of D/2 is initially set-up. The sediments and hydrodynamics are similar as the 3DScour configuration.
Boundary and initial conditions
The boundary conditions are very close to the 3DScour configuration :
(i) At the inlet, vertical profiles obtained from a 1D vertical simulation are imposed for . Zero transverse velocity is prescribed.
(ii) At the outlet, Neumann boundary conditions are specified for all quantities, except for the pressure for which a homogeneous Dirichlet boundary condition is imposed for the reduced pressure. For the velocities, a homogeneous Neumann boundary condition is used when the velocity vector points outside of the domain at the outlet, and a homogeneous Dirichlet boundary condition is used otherwise.
(iii) At the top and side boundaries, the same boundary conditions as in the 3DScour case are used.
(iv) At the walls (including the cylinder), zero velocity (no-slip) is imposed for the three components and a small value is imposed for the turbulent kinetic energy (TKE) k.b. The boundary condition for is specified using the classical wall function from openFOAM at the cylinder and using a constant value is imposed at the bottom.
Physical properties
The transportProperties file for the 3DScourSqr is identical to the 3DScour configuration.
Kinetic theory
In this tutorial, the kinetic theory is used for the granular stress model and the kineticTheoryProperties reads:
kineticTheory on; limitProduction off; extended off; e e [ 0 0 0 0 0 0 0 ] 0.7; muPart muPart [ 0 0 0 0 0 0 0 ] 0.4; alphaMax alphaMax [ 0 0 0 0 0 0 0 ] 0.635; MaxTheta MaxTheta [ 0 2 -2 0 0 0 0 ] 0.5; phi phi [ 0 0 0 0 0 0 0 ] 32; psi psi [ 0 0 0 0 0 0 0 ] 0.0; killJ2_ killJ2_ [ 0 0 0 0 0 0 0] 0; quadraticCorrectionJ1_ quadraticCorrectionJ1_ [ 0 0 0 0 0 0 0 ] 1; viscosityModel GarzoDuftyMod; conductivityModel GarzoDuftyMod; granularPressureModel Lun; saltationModel none; radialModel ChialvoSundaresan;
Turbulence properties
The turbulence model is set to twophasekOmegaSAS in turbulenceProperties.b:
simulationType RAS;
RAS
{
RASModel twophasekOmegaSAS;
turbulence on;
printCoeffs on;
twophasekOmegaSASCoeffs
{
alphaOmega 0.52;
betaOmega 0.0708; // original k-omega: 0.072 // k-omega (2006): 0.0708
C3om 0.35;
C4om 1.0;
alphaKomega 0.6; // original k-omega: 0.5 // k-omega (2006): 0.6
alphaOmegaOmega 0.5;
Clim 0.875; // original k-omega: 0.0 // k-omega (2006): 0.875
sigmad 0.125; // original k-omega: 0.0 // k-omega (2006): 0.125
Cmu 0.09;
KE2 1.0; //turb modulation
KE4 1.0; //density stratification g
nutMax 5e-3;
popeCorrection true;
delta vanDriest;
vanDriestCoeffs
{
delta cubeRootVol;
cubeRootVolCoeffs
{
deltaCoeff 1;
}
Aplus 26;
Cdelta 0.158;
}
}
}Control
The system/controlDict file indicates that for this case the time step is fixed at 0.0005 s.
Computation launching
As for the previous case, you can launch the computation by executing * Allrun *. The mesh is quite coarse and the simulation can be launched with 10 cores.
Post-processing using paraview
The post-processing is mostly performed using paraview. No python script is provided within configuration at the moment. A snapshot of the simulation with the hybrid model is shown next: